Zachary's Karate Club Technical Journal 2

The Problem:

  My last technical journal for this dataset can be found on the home page but here's a short
summary: Zachary’s Karate Club is a social network of a karate club that captures 34 members and records links with pairs of interacting members as edges. During the study, the karate club had split into two (between John and Mr. Hi), coincidentally also dividing the members into the two factions. The task at hand is to determine/predict which members would stick with John or leave with Mr. Hi.


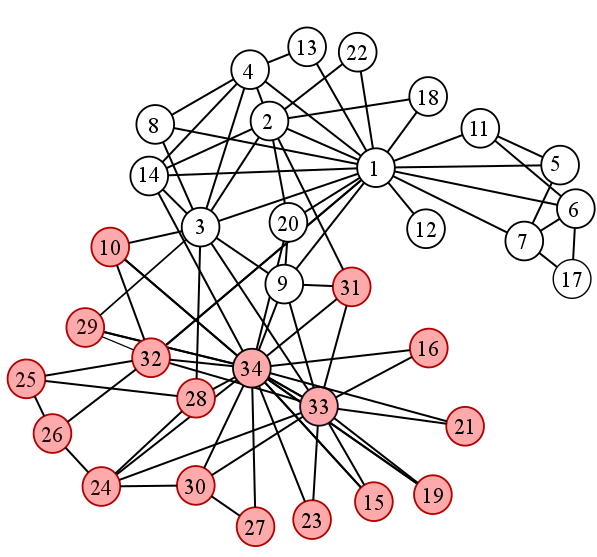
This is an example of an algorithm splitting the 34 members into two groups, indicated by the color difference

The Algorithm:

Previously I've tried many algorithms like K-nearest-neighbor but all of those have proven not
applicable to this graph dataset. However, I was fortunate enough to have found an algorithm that
sounds promising: Community Detection/Girvan-Newman Algorithm. Here's a basic rundown on how the code works:
Girvan-Newman Algorithm (Input: A weighted graph G, Output: A list of components of G):
  1. BestQ = 0
  2. Convert the edge matrix into a weighted (0 or 1) social graph G
  3. Compute the number of components of the graph G (init_ncomp)
  4. Calculate the weighted version of edge-betweenness for all edges of the graph G
  5. Find the edge with the highest betweenness and remove it from G
  6. Compute the number of components in G after edge removal (ncomp)
  7. If ncomp <= init_ncomp go to back to step 3
  8. Compute the modularity of the current version of graph G and store it in Q
  9. If Q > BestQ then saves the current decomposition of G as the best division in BestComps
  10. If there is not any edge left in G return BestComps otherwise go back to step
For a demonstration on how it works, you can find a video here: 
Video showing how Girvan-Newman works on a simple graph
Image result for community detection
The diagram is a comparison between K-means’ and Spectral’s results.

The Results:

The model had around 94% accuracy with the only nodes being missed are 2 and 8 (indicated
in the red rectangle). I cannot blame the algorithm because so many other models have also
mistaken those two for another cluster. Also, I dropped NMI as a way to display how accurate a model
was because determining that value is fairly simple.
Above is what Community Detection predicted

In The Future:

Prior to this edit, I could not get it to work but the error just happened to me forgetting to terminate
a while-loop. In the future, I would like to find more algorithms to test for compatibility. I can conclude
this algorithm a success for now.

Comments

Post a Comment

Popular posts from this blog

Technical Journal - Research Papers

Image
On the Efficiency of Data Collection for Crowdsourced Classification :        The paper aims to explain the accuracy gaps between popular collection policies (state-action mapping) on crowdsourced data. The quality of crowdsourced data is often highly variable so it is suspected that it is the cause. However, studies show that the policies used to collect such data have a strong impact on the accuracy of the system. The first theoretical explanation of the accuracy gaps is that the non-adaptive uniform allocation, and the adaptive uncertainty sampling and information gain maximization. Done with the representation of the collection process in terms of random walks in the log-odds (log of odds of guessing correctly/incorrectly) domain, the author derives lower and upper bounds on the accuracy of the policies. The bounds accurately tell us by how much do two adaptive policies trump a non-adaptive one. It is believed that techniques used by them are applicable to addi...
Read more

Journal

Image
On Tuesday, March 24th, we had a meeting with Professor Hassibi over Zoom. Prior to our talk, we had issues with our code regarding the fact that it didn't produce the results expected. He told us to find and graph the eigenvalues of the graph Laplacian, as that would indicate the number of clusters found and value you can refer other datapoints to. He noted that graphing the corresponding eigenvector would indicate whether a cluster had been isolated or not. On that note, it was up to us to tinker with values for a bit and try different algorithms like K-means. Below is a video of the meeting with Professor Hassibi: This week has been very interesting, to say the least. As you may know, COVID-19 has just taken the U.S. for a turn and has put a pause on daily life, forcing businesses to adapt, overcome, or fail in some cases. For us high schoolers, classes have migrated to the Zoom platform. With it followed teachers with bad internet service, leading to indecipherable dialect...
Read more

First Month

Image
The first four weeks of this Caltech Stem class have been interesting, to say the least. Much of the material we went into have been all over the place with various objectives. We started off with teamwork exercises, watching college students present their research, replicating one for ourselves, writing a concept map, and going to Caltech to meet Dr. Hassibi. We had two, teamwork workshops for the first two weeks. One of which was the dominoes problem where each student was given two dominoes and we were instructed to get three dominoes per person by exchanging dominoes for chips and chips for dominoes. Instructions were very vague other than that everyone must have a domino to "survive" a round. We struggled in the first few attempts but through several days of discussion and trial & error, we were able to find a way to accomplish our goal. Some key underlying goals of this exercise were the importance of leadership, communication, and open-mindedness...
Read more