Zachary's Karate Club Technical Journal 1
The Problem:
The data set we needed to correctly predict was Zachary’s Karate Club, a social network of a university karate club studied by Wayne W. Zachary between 1970 and 1972. The network captures 34 members of a karate club and records links with pairs of interacting members. During the study, the owner of the club, John A, and instructor, Mr. Hi, had an argument and decided to part ways from each other. This effectively split the 34 members into two: half of them left for Mr. Hi’s new company and the rest either found a new instructor or quit the sport. The task at hand is from a data set, determine which members would stick with John or leave with Mr. Hi.
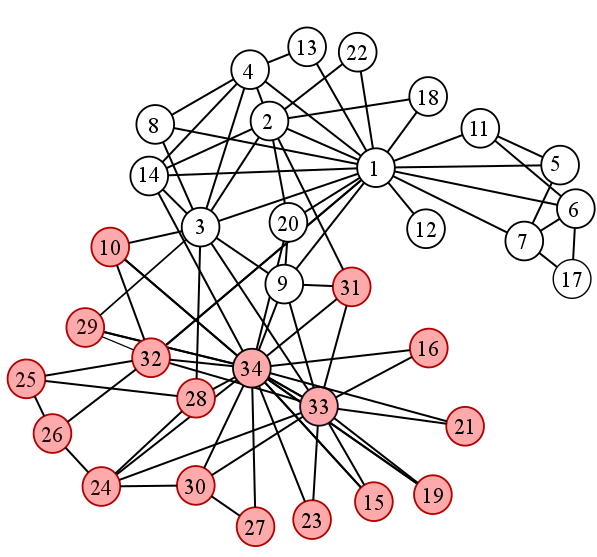
The Data:
The data, in its simplest form, is a graph that has 34 nodes, each one representing one member. The nodes have a node attribute ‘club’ that indicates the name of the club to which the member represented by that node belongs, either ‘Mr. Hi’ or ‘Officer’. The code to extract the data is G = nx.karate_club_graph(). Since we will be testing multiple clustering methods on the data, we need a control, the ground truth of who went where to be exact. The ground truth is this: [0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1, 0, 0, 1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]. Both of these data are important because the nx.karate_club_graph() gives us data to test algorithms on. We then compare how it did with the actual outcome of the split, which is the ground truth array. We used the spring_layout function from networkx to the data so that when we plot the graph, it will look “nice”. The code is pos = nx.spring_layout(G) which essentially positions nodes using the Fruchterman-Reingold force-directed algorithm. We also used a method to create an “edge mat” from G which is a 2d array using 0 and 1 to display connects between nodes.
The Algorithm:
I used/tested the data set with Spectral Clustering, a technique with roots in graph theory, where the approach is used to identify communities of nodes in a graph based on the edges connecting them. Spectral clustering uses information from the eigenvalues (spectrum) of special matrices built from the graph or the data set. I used an adjacent matrix where the rows and columns represent nodes with the entries representing if they have a connection or not (0 or 1). I chose this algorithm because it was highly recommended by websites due to its “simplicity” and flexibility. But mainly because it was a graph clustering algorithm, not a distance-based one which is what K-means is. We used K-means at the beginning, but we soon realized that these points, while plotted based on their relationships, should not be clustered by their distance. This caused us to go back to our drawing board to discuss possible algorithms. Connection-based algorithms, however, are more applaudable but perform differently.

The Results:
The data set we needed to correctly predict was Zachary’s Karate Club, a social network of a university karate club studied by Wayne W. Zachary between 1970 and 1972. The network captures 34 members of a karate club and records links with pairs of interacting members. During the study, the owner of the club, John A, and instructor, Mr. Hi, had an argument and decided to part ways from each other. This effectively split the 34 members into two: half of them left for Mr. Hi’s new company and the rest either found a new instructor or quit the sport. The task at hand is from a data set, determine which members would stick with John or leave with Mr. Hi.
This is an example of an algorithm splitting the 34 members into two groups, indicated by the color difference
The data, in its simplest form, is a graph that has 34 nodes, each one representing one member. The nodes have a node attribute ‘club’ that indicates the name of the club to which the member represented by that node belongs, either ‘Mr. Hi’ or ‘Officer’. The code to extract the data is G = nx.karate_club_graph(). Since we will be testing multiple clustering methods on the data, we need a control, the ground truth of who went where to be exact. The ground truth is this: [0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1, 0, 0, 1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]. Both of these data are important because the nx.karate_club_graph() gives us data to test algorithms on. We then compare how it did with the actual outcome of the split, which is the ground truth array. We used the spring_layout function from networkx to the data so that when we plot the graph, it will look “nice”. The code is pos = nx.spring_layout(G) which essentially positions nodes using the Fruchterman-Reingold force-directed algorithm. We also used a method to create an “edge mat” from G which is a 2d array using 0 and 1 to display connects between nodes.
The Algorithm:
I used/tested the data set with Spectral Clustering, a technique with roots in graph theory, where the approach is used to identify communities of nodes in a graph based on the edges connecting them. Spectral clustering uses information from the eigenvalues (spectrum) of special matrices built from the graph or the data set. I used an adjacent matrix where the rows and columns represent nodes with the entries representing if they have a connection or not (0 or 1). I chose this algorithm because it was highly recommended by websites due to its “simplicity” and flexibility. But mainly because it was a graph clustering algorithm, not a distance-based one which is what K-means is. We used K-means at the beginning, but we soon realized that these points, while plotted based on their relationships, should not be clustered by their distance. This caused us to go back to our drawing board to discuss possible algorithms. Connection-based algorithms, however, are more applaudable but perform differently.
The diagram is a comparison between K-means’ and Spectral’s results.
The Results:
The following two pictures are what K-means and Spectral produced respectively. From careful observation, it is noted that the node in the middle of the graph is different in each result. Which algorithm correctly assigned the nodes we don’t know for sure unless we look at the ground truth. This result must’ve been that Spectral believed that that node had more relationships with the nodes labeled “blue” than with those labeled “green”. However, we need to compare the results to what actually happened, which is why we use an NMI score to come to the conclusion of which algorithm did better.


As you can tell from the image below, K-means did better than Spectral with one node difference. Still, it was not good enough. It still baffles us, the students, why K-means does so well. I propose it is because we use the spring_layout function. That gives the nodes their x and y values on the graph, but I believe that the values are dependent on the relationships between the nodes, plotting nodes closer to each other if they are related.

In The Future:
On my own, I will be testing K-nearest-neighbors, another graph clustering algorithm. My progress as of today, 10/9/19, is small because I need to adapt the data to the algorithm’s needs. I previously tried to do Markov Clustering but for some reason I had struggles importing the libraries necessary.
Above is what K-means predicted
Above is what Spectral predicted
NMI Score for the two algorithms we used
In The Future:
On my own, I will be testing K-nearest-neighbors, another graph clustering algorithm. My progress as of today, 10/9/19, is small because I need to adapt the data to the algorithm’s needs. I previously tried to do Markov Clustering but for some reason I had struggles importing the libraries necessary.


Comments
Post a Comment